
Next: Homography Up: Miscellaneous notes Previous: Voronoi tesselation on a Contents
 . As the orthogonal set of sinc functions
. As the orthogonal set of sinc functions
 sinc
sinc
 , an analog signal can be (uniquely) produced from a digital signal of length
, an analog signal can be (uniquely) produced from a digital signal of length 
![$\displaystyle \{ x[n]\}_{n=0}^{N-1}
$](img110.svg)
![$\displaystyle S(t) =\sum_{n = 0}^{N-1} x[n]$](img111.svg) sinc
sinc
 is the sampling rate of the digital signal.
is the sampling rate of the digital signal.
The following GNU Octave function produces the analog signal from a given digital signal
%%Function returns the values at times T of the analog signal of the corresponding digital signal sampled at speed Fs.
function xb = digitaltoanalog(T, digitalsignal, Fs)
xb = [];
for t = T
xb = [xb sum(digitalsignal.*sinc(Fs*t - (0 : length(digitalsignal) - 1)))];
end
end
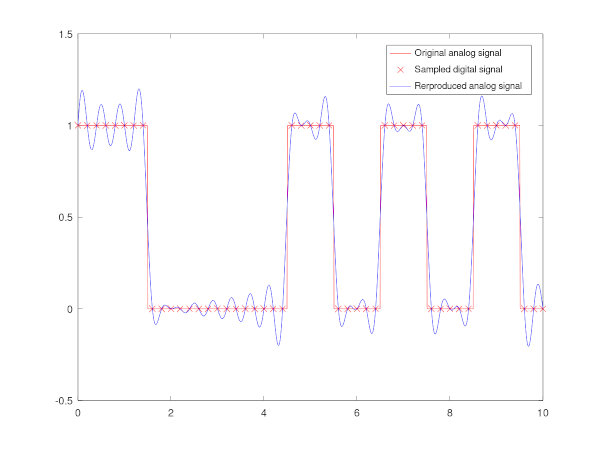
The following code simulates a rectangle pulse train signal given as input, samples the input to a digital signal 



pkg load signal; close all; clear all; input = @(t) pulstran(t,[0,1,5,7,9],"rectpuls") %%The original analog signal at time t. Fs = 5; %Sampling rate. t = 10 %Time length of the signal. Ts = 0 : 1/Fs : t; %Sampling time instances. x = input(Ts); %Sampled values, i.e. the digital signal. Ta = linspace(0, t, 1000); %Analog signal time instances for the plot. S = digitaltoanalog(Ta, x, Fs); %Modulated analog signal. %Plot. plot(Ta, input(Ta), 'color', 'r'); hold on; plot(Ts, x, 'x', 'color', 'r') plot(Ta, S, 'color', 'b'); legend( 'Original analog signal','Sampled digital signal', 'Rerproduced analog signal')
References: