
Next: May – Digital to Up: Miscellaneous notes Previous: Inverse of a Gaussian Contents
Voronoi tessellation consists of neighborhood areas of a given set of points, or Voronoi cells: every cell is surrounded by the area that consists of locations that are closer to the cell than any other cell. The Voronoi Diagram, or Voronoi tessellation, has applications, e.g., in wireless communications.
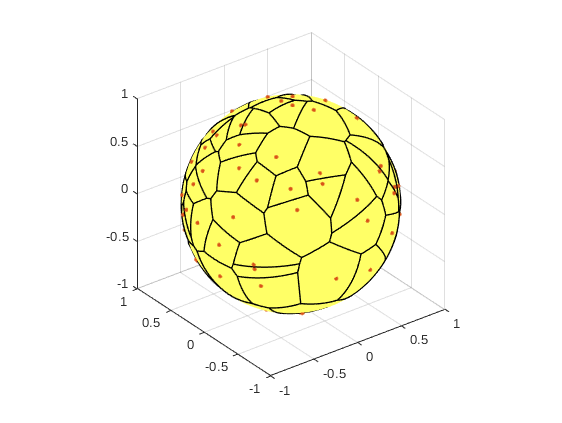
The next Matlab code produces a Voronoi tessellation on a sphere Poisson points as cells. It is based in Grady Wrights codes openly available in Github.
%%Create Voronoi tesselation around Poisson points on a Sphere.
clear all;
close all;
addpath(fullfile(cd,'rbfsphere'));
density = 100;
X = poissononsphere(density)'; %Poisson points in spherical coordinates.
voronoiSph(X); %This function is downloaded from gradywright's Github. It is placed in the folder 'rbfsphere'.
function refc = poissononsphere(density)
yMin = -1; yMax = 1;
xMin = -pi; xMax = pi;
xDelta = xMax - xMin; yDelta = yMax - yMin; %Rectangle dimensions
numbPoints = poissrnd(density); %Number of points in the area is a Poisson variable of intensity given as density
x = xDelta*(rand(numbPoints,1)) + xMin; %Pick points from uniform distribution
y = yDelta*(rand(numbPoints,1)) + yMin; %Map referencepoints to geographical coordinates
ref = [x y]';
refs = [x'; asin(y)'];%Map geographical coordinates to Cartesian coordinates on a unit circle
r = 1;
refc = [r*sin(refs(2,:)+pi/2).*cos(refs(1,:)+pi);...
r*sin(refs(2,:)+pi/2).*sin(refs(1,:)+pi);...
r*cos(refs(2,:)+pi/2)];
end
References: