
Next: Blog posts 2021 Up: Blog posts 2022 Previous: Blog posts 2022 Contents
Noise is often modeled to have a Gaussian waveform. However, it might be unrealistic in some circumstances if the outlier events are more likely than in the Gaussian distribution. In this case, we might have to model the noise with fat-tailed distributions with significant mass in the tail distribution.
The 




Other impulsive noise distribution models are the Middleton distributions representing the envelope of non-Gaussian electromagnetic noise.
In the following, we compare the Gaussian and 




pkg load statistics
clear all;
close all;
%%Function returns the values at times T of the analog signal of the corresponding digital signal sampled at speed Fs.
function xb = digitaltoanalog(T, digitalsignal, Fs)
xb = [];
for t = T
xb = [xb sum(digitalsignal.*sinc(Fs*t - (0 : length(digitalsignal) - 1)))];
end
end
%%Inverse of the alpha stable CDF with alpha = 1.
invalphaCDF = @(x) tan(0.5*(-1 + 2*x)*pi);
%%Generate N Alpha-stable samples.
N = 100;
alphasamples = invalphaCDF(unifrnd(0,1,1,N));
%%Generate normal samples.
normalsamples = normrnd(0,1,1,N);
%%Convert to analog signal.
T = 1 : 0.1 : N;
alphasamples = digitaltoanalog(T, alphasamples, 1);
normalsamples = digitaltoanalog(T, normalsamples, 1);
alphasamples = alphasamples/(mean(abs(alphasamples))); %Normalize by mean instantaneous amplitude.
normalsamples = normalsamples/(mean(abs(normalsamples)));
figure(1)
plot(T, alphasamples)
legend('Alpha-stable noise')
axis([0 100 -15 15])
figure(2)
plot(T, normalsamples)
legend('Gaussian noise')
axis([0 100 -15 15])

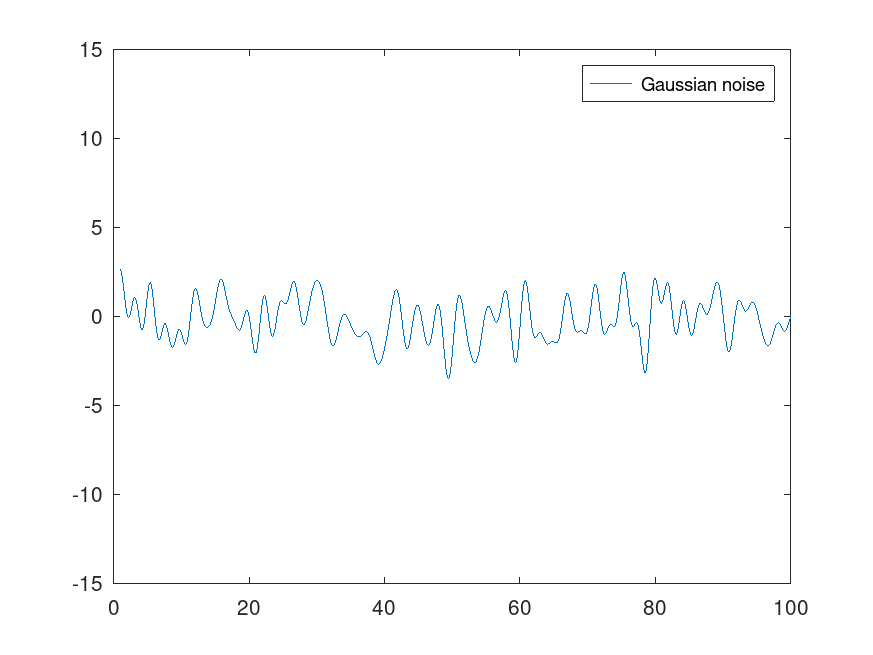
Comparing the figures, one can easily understand where the term “impulsive noise” comes from.
It is also interesting to compare the audiolized noise signals: my Soundcloud.
References: